Windил энергиясе математика исәпләүләре
- җил турбинасының сөртелгән мәйданын үлчәү
Кычкыру өлкәсен үлчәя белүтеләсәгез, сезнең пычаклар мөһимҗил турбинасының эффективлыгын анализлагыз.
Коткарылган өлкәпычаклар белән ясалган түгәрәкһава аша сөртү.
Кычкырып, бер үк кулланыгызРайонны табу өчен сез кулланган тигезләмәТүбәндәге түгәрәк табылырга мөмкин
Тигезләмә:
Мәйдан = πc2
-
π = 3.14159 (PI)
r = түгәрәкнең радиусы. Бу сезнең пычакларның озынлыгына тигез.
-
-
-
-
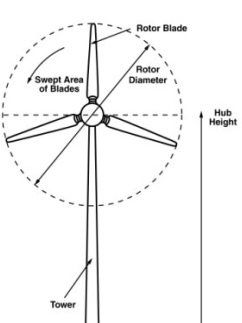

- Ни өчен бу мөһим?
Сезгә сөртелгән урынны белергә кирәк булачакГомуми көчен исәпләү өчен җил турбасыСезнең турбинага бәрелгән җил.
Windил тигезләмәсендә көчен исегездә тотыгыз:
P = 1/2 x ρ x A x V3
-
P= Көч (ват)
ρ= Һава тыгызлыгы (диңгез дәрәҗәсендә якынча 1,225 кг / м3)
A= Пычракларның сөртегез (M2)
V= Җил тизлеге
-
-
Бу исәпләү эшләп, сез билгеле җил өлкәсендә гомуми энергия потенциалын күрә аласыз. Шуннан соң сез моны җил турбинасы белән җитештергән көчнең күләме белән чагыштыра аласыз (сезгә моны мультимортер белән тапкырлау ярдәмендә бер тапкыр күп көч арттыру ярдәмендә исәпләргә кирәк).
Бу ике санның чагыштыру сезнең җил турбинасы никадәр нәтиҗәле икәнен күрсәтәчәк.
Әлбәттә, җилегезнең киң таралган мәйданын табу - бу тигезләмәнең мөһим өлеше!
Пост вакыты: Апр-18-2023

